August 2023: let's try writing a newsletter again
"Season 3" of whatever this is
I learned a clever trick from Robin Sloan, which is that when you get bored of writing a newsletter you can declare that it’s “the end of Season N” and just drop it. Then if you feel inspired to pick it up later, you can send another one and call it “the start of Season N+1”. I’d done the dropping-and-picking-it-up-again routine once before, but this season language makes it seem way more legit. So welcome to Season 3. If you have no memory of what the hell this is and want to get rid of it, please press the Unsubscribe button :)
The main thing that prompted the new start is that I gave up on Twitter because it had got too crap. There are a lot of things I miss about it, so maybe I’ll be back, but certainly for the next few months it seems unlikely that I’ll bother with it. I’ve had more time to think because I’m not staring at so much nonsense on a screen, but also I’ve been missing having some kind of public outlet for going on about stuff. Anyway I’m suddenly excited about this format again. This one’s kind of rushed because I only had the idea late in the month, but hopefully I’ll enjoy doing some more of these.
Qubit phase space, AGAIN
I’m back thinking about physics. All the same stuff as before: negative probabilities, quantum physics on phase space, bla bla bla. It’s currently hard to tell whether I’m actually getting anywhere or doing anything useful. Instead it feels like I’m sort of going around the houses reminding myself where everything is. I’m thinking about things in a slightly different way, though, so maybe I can talk about that.
So, quantum physics on phase space. This is what it sounds like: quantum physics, but formulated on phase space (a space with position and momentum coordinates, pretty much). It’s a bit different to the standard Hilbert space way of thinking about QM and not normally taught in an undergrad course, though it’s pretty well used in some specific fields like quantum optics. I personally never learned it until I got interested in this negative probability stuff a few years ago.
I like quantum physics on phase space because it’s also common to do classical physics on phase space. This makes the differences to classical physics pop out nicely. By comparison, in the normal Hilbert space formulation you have to keep track of which weird bits are the mathematical formalism being different to classical physics and which weird bits are actual results.
In classical statistical physics you can define probability distributions over phase space. Quantum physics can be set up on phase space in a very similar way, with a function called the Wigner function that looks sort of like a probability distribution. The difference that makes it weird is that the “probabilities” can go negative. (This doesn’t affect anything you can actually observe, because in quantum physics you never observe both the position and momentum at once. The probabilities of things you observe are normal, positive ones.)
The slightly different way I’m thinking about phase space this time is something like… normally the phase space formulation is “built out of” the basic components of the Hilbert space one. E.g. the core object that describes a system’s state in the phase space formulation is the Wigner function, whereas in Hilbert space the core object is something called the density matrix. Normally the Wigner function is written out in terms of the density matrix. But, instead, you could think about how it matches directly to physical observables in the same way you match the wavefunction to observables, without taking this detour. Getting good at thinking in these way seems useful for really inhabiting the phase space view of the world.
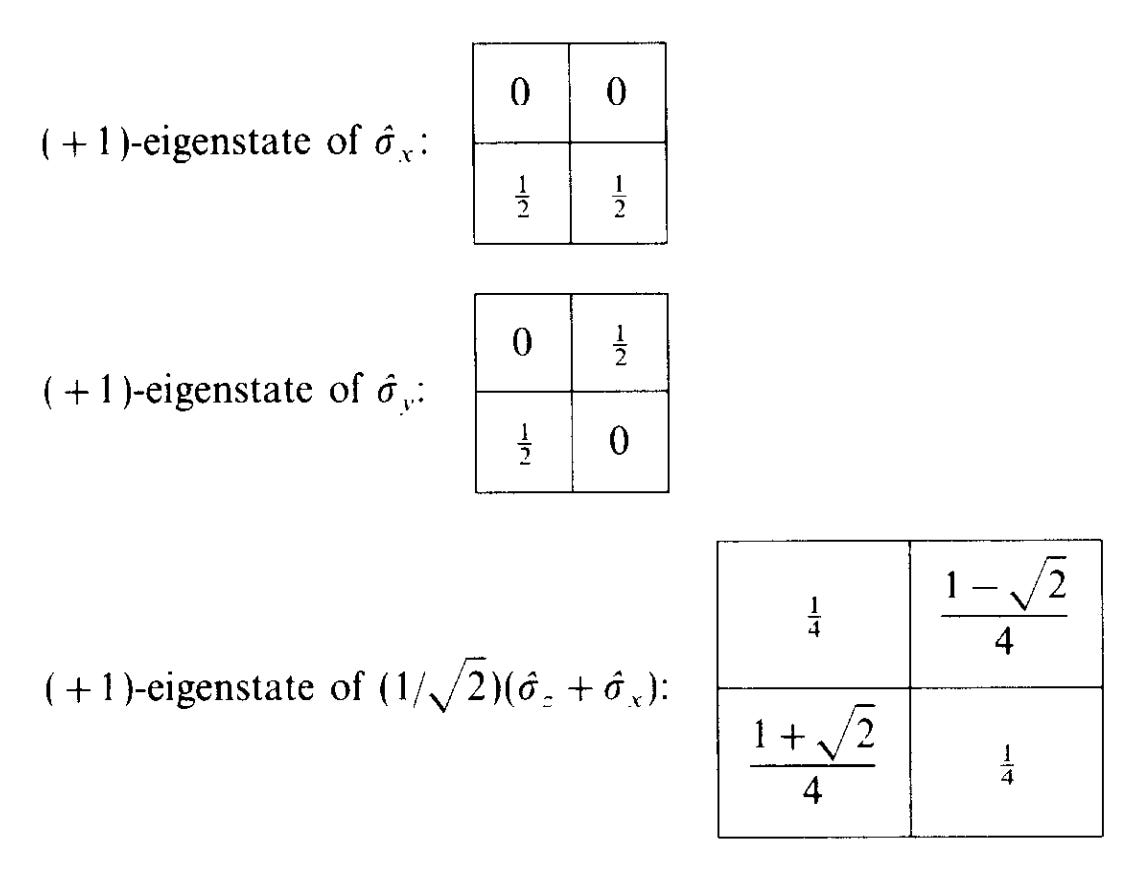
I mostly think about qubit phase space, because a qubit is the simplest system going. Qubits only have two position states, 0 and 1, and two momentum states, 0 and 1, so qubit phase space just has four points. And then probability distributions over them look like boxes of four numbers, like these:
These are from A Wigner-function formulation of finite-state quantum mechanics by Wootters. Notice the negative number in the top right of the last one. The coordinates aren’t labelled, but position (which is normally labelled z for Reasons) is along the bottom and momentum (normally labelled x) is up the side.
You can’t directly observe the probabilities in the four boxes, because you can’t observe both position and momentum at once. Instead, you can observe marginal probabilities, sums over the rows, columns or diagonals of the boxes. These are always positive. So in this phase-space-first view of a qubit, you can think of it in terms of the three sums along the right column, top row and top-left-to-bottom-right column, which I’ll call q_z, q_x, and q_y:
Notice that those three conditions in the brackets are a mutual contradiction. You can’t have something where x is always 1, and z is always 1, and x xor z is also always 1. We only want them to hold probabilistically, so this isn’t necessarily a problem, but you can see that it would be bad if you put “too much probability” into them - if you set all three qs to 1, for example, so that all three always hold, you’d have a contradiction. The constraint to avoid the “too much probability” problem is:
(See this paper for details on how to derive these sort of constraints.)
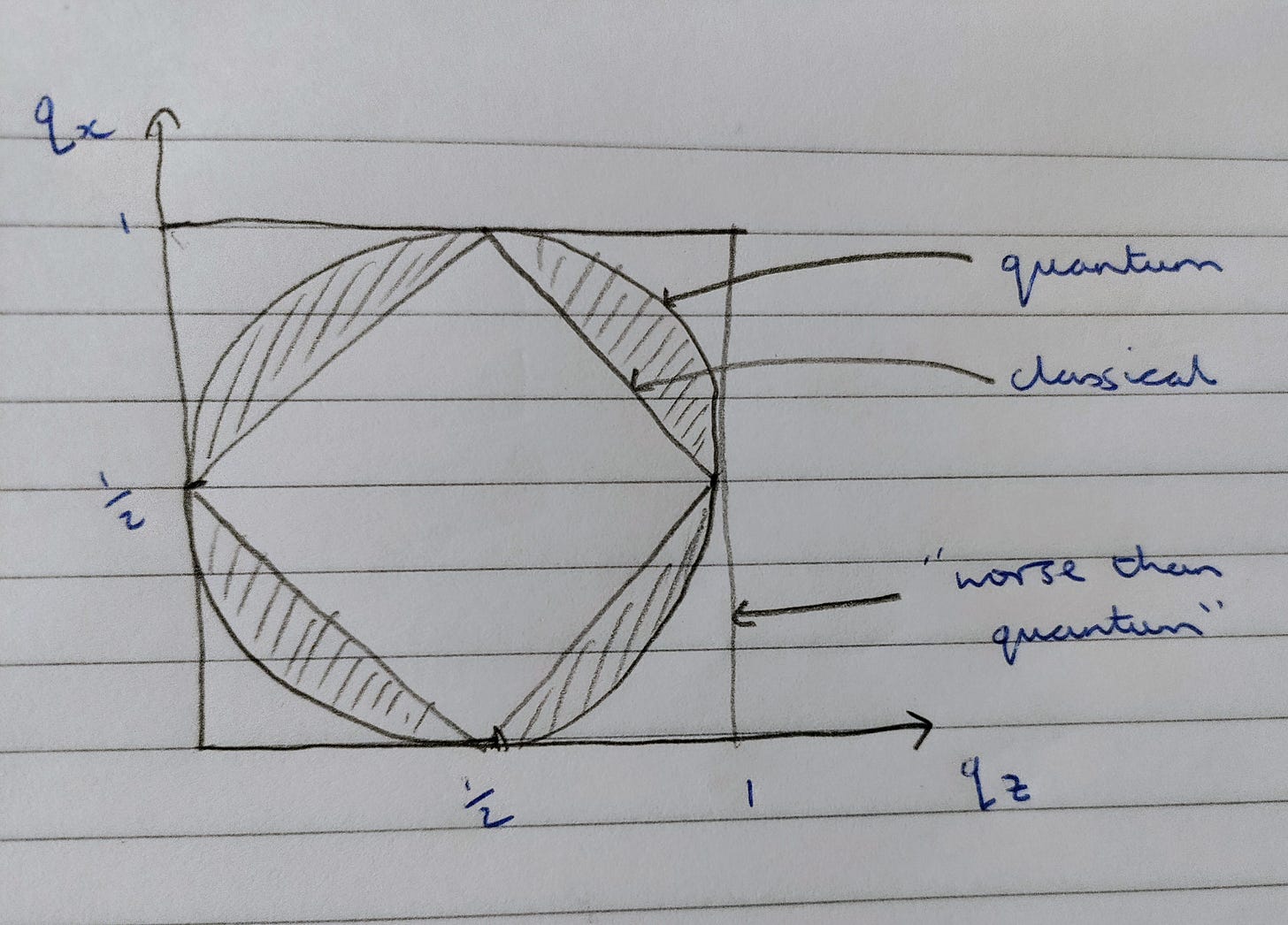
Classical physics sticks to this constraint. Though it’s actually more complicated: there are eight of these inequalities, one for each permutation of 0s and 1s for the logical conditions, leading to an octahedron of allowed states in the middle. (Three other permutations are also contradictions, so you get a different “avoiding too much probability” less-than inequality. The other four permutations are not contradictory, but instead you have to make sure you’re putting enough probability in, so you get a greater-than inequality).
Quantum physics pushes past the constraint, indicating that whatever these quantum measurements are doing, it’s not just a passive reading-off of three already-existing properties. I’ve talked about Bell’s theorem before, but to me qubit phase space has a very similar core of quantum weirdness in a simpler setting, with the same sort of too-much-probability problem underlying the weirdness.
It’s not arbitrary amounts of weirdness, though. You can’t pick whatever you like for the qs, there’s still a constraint:
So you get a sphere of points with radius of 1/2, centred on (1/2, 1/2). I’m not going to attempt to draw the octahedron and sphere, but here’s a quick crappy sketch of a slice through the middle:
The qubit states that have negative probabilities all live in the shaded bit, between the classical and quantum constraints.
I also drew a box around the edge, to represent hypothetical systems like the one I talked about in Worse than quantum physics that just maxes out the contradiction by setting all the qs to 1. (I originally got it from this blog post by Dan Piponi.) You could think of extending this to a whole cube of worse-than-quantum-physics states that are as bad as possible.
(If you know about norms on metric spaces, you might recognise the 1-norm, 2-norm and ∞-norm here. E.g. see this diagram. Scott Aaronson likes to introduce quantum physics as a theory based on the 2-norm, and this is another manifestation of that.)
So quantum physics is weird, but a constrained kind of weird rather than as weird as possible.
OK, so we’ve gone round the houses looking at things again. Maybe next time I’ll get onto something new. I might also try writing this up a bit better and posting it as a standalone blog post.
Other things
I only decided to do this pretty late in the month, so I have no notes, but this is what I remember:
I read Cal Newport’s Digital Minimalism. It says exactly what you’d expect it to say if you’ve ever read anything else by Cal Newport. Ironically I mainly read it because I’m missing my normal stream of Twitter text, and Newport’s stuff “feels like the internet” to me, probably because I read his blog before any of the books. I then reread Venkatesh Rao’s Against Waldenponding as a counterpoint and had a rush of nostalgia for the glory days of 2018 when the giant social computer in the cloud was in a better state. I like being part of the “great computational fluidization of human cognition”, and writing the odd blog post or newsletter doesn’t really cut it :(
I also read a couple of fun fiction books about swamps. I’ve been looking for something with a similar feel to Swallows and Amazons, and I remembered Gone-Away Lake by Elizabeth Enright, a favourite book when I was a kid, set in an abandoned nineteenth-century resort on the edge of what used to be a lake and is now a muddy bog. This was a good choice, it has the right sort of competent-people-doing-practical-things plot and lots of detailed descriptions of fixing up buildings and moving furniture and so on. Then the setting reminded me of A Girl of the Limberlost, a 1910 book which takes place around the former Limberlost swamp in Indiana, and that was also well worth rereading. It’s a ridiculous melodrama with a nonsense plot based around catching moths, and I loved it.
I’m getting very into learning music theory. These videos are great. May infodump about it at some point.
I wrote a notebook post on how to use a foot massage roller as an awareness expansion cue.
Next month
No idea. Probably more physics, because that’s what I’m mostly thinking about right now. Also if I read something interesting I’ll talk about that.


Nice to read you again! Twitter is lost, but we’re all still somewhere.