July 2021: Drawing Theories Apart offcuts
Bubble chambers and loops
So, after last month’s excuse note my plan was to do a decent newsletter this time. I started early, meaning to talk about David Kaiser’s Drawing Theories Apart, a history of Feynman diagrams in physics. It came out looking more like a standalone blog post so I decided to post it there instead, and now it’s the last day of the month and I still have to write a newsletter. Ah well.
I’m going to take the easiest option and cover a couple of other bits from the book that I didn’t get to in the review. The first one is a fairly straightforward point about bubble chambers, the second is a physics-heavy confused braindump.
Bubble chamber pictures
There’s an interesting section about bubble chambers. These were a 1950s invention that allowed charged particles to be detected through the ionization track they made in liquid hydrogen. The liquid vaporises along the track, creating visible paths of bubbles that could be photographed:
[source]
Kaiser is trying to understand why Feynman diagrams spread so fast as a method through disparate fields of physics, and he speculates that these tracks had something to do with it:
One locus to consider is the inundation of nuclear and particle physicists during exactly this period with nuclear-emulsion and bubble-chamber photographs… To physicists in the 1950s and 1960s, photographs of these new particles from nuclear emulsions and bubble chambers were simply inescapable: they were published with articles in the Physical Review, on the covers of Physics Today, cataloged in huge atlases, reprinted on the dust jackets and frontispieces of textbooks and popularizations, and pictured on slides for public lectures… Moreover, there developed in this period a highly schematized tradition of reconstructing particles’ paths, as photographed with the new detectors.
Maybe that seems like a stretch from the picture above, but look at this one from the book:
These really do look quite a lot like Feynman diagrams! No physicists were claiming that these tracks were ‘the same thing’ as Feynman diagrams, but the visual language of vertices and propagation lines is strikingly similar.
What are the loops about?
This part is the physics-heavy confused braindump, i.e. it’s very skippable if that’s not what you want.
At the end of the review I wrote this:
Since reading Helling’s notes on Feynman diagrams in classical physics, I’ve been curious about how they connect to the quantum versions. There’s a big difference between the classical and quantum diagrams – the quantum ones have loops and the classical ones don’t – and I’d like to understand why this happens at a deeper level, but it’s kind of hard to compare them properly when the formalisms used are so different.
I’m going to attempt to explain this better in this section. But I won’t explain it very well, because I don’t have a very clear understanding of what I’m even asking yet. Maybe writing it down will help a bit.
So, there’s a particular example of a quantum field theory called scalar ϕ^4 theory. It’s not the most useful theory, but it’s more straightforward to calculate with than most, so it comes up a lot as a teaching example. When I was trying to learn some QFT a while back (out of Lancaster and Blundell’s Quantum Field Theory for the Gifted Amateur, an excellent book with a weird name) I mainly worked through this example.
The classical example in Helling’s notes has the same quartic interaction term as the ϕ^4 theory, so I’d like to compare them. But the quantum version also has all this extra quantisation stuff, like operators and so on, so it’s hard to compare them like for like. I’d enjoy seeing everything in the same notation, which I guess means either getting operators into the classical version or taking them out of the quantum one.
I wondered about this a few years ago but never spent enough time to take it very far. Reading the section of the Kaiser book that talked about the differences between Feynman’s and Dyson’s view of what Feynman diagrams mean, I found the following:
A closer look at Feynman’s famous pair of articles from 1949 bears this out… The treatment in this first article was entirely divorced from QED: the electrons and positrons either propagated freely, subject to no interactions, or traveled in a fixed, classical, external field. Using these spacetime pictures, Feynman developed his “kernel” methods with a series of semiclassical examples of electrons’ motion - semiclassical because he treated the electrons and positrons quantum-mechanically, but the electromagnetic potential classically.
This sounded like it would be more useful for comparing to the classical case, but I know the early QED papers are all really difficult to read. But after some more googling, I found a textbook, Quantum Field Theory by Michael Sadovskii, that follows the same approach. This actually does look fairly approachable, in fact it starts with a fairly straightforward looking nonrelativistic example. So, if I decide I’m interested enough in this topic, I should be able to work through that.
Now let’s dump my remaining thoughts on the topic in an even more disorganised form. There’s a load of stuff about the propagator I don’t understand well (the propagator is the integral kernel mentioned in the quote above, known as a Green’s function or fundamental solution in other situations). Helling doesn’t say much in his notes about what propagator is being used, but for the classical case I assume it’s the retarded propagator, which only propagates between x and y if y is to the future of x. Whereas QFT uses the Feynman propagator, which is a sort of mix of the retarded propagator with an advanced propagator (which does the opposite).
This propagator stuff intuitively seems relevant - like, if the propagator only propagates forward, you can’t get loops, right? But I don’t understand the details. Again, I might pick up something useful from the Sadovskii book, though.
If anyone persevered through this braindump and can point me at something that will help me become less confused, please let me know.
Next month
August is supposed to be the transitional month for me where I stop just fiddling around with what random project comes to mind and start thinking about jobs and so forth. It doesn’t have to be an abrupt transition, but needs to happen some time soonish.
My default option is to start applying for programming jobs, but I’m still pretty undecided on what I’d like to do, so I guess this would be a good place for what I previously called a call for perturbations:
So, I’m trying to figure out what to do next. This section is a call for perturbations, which is a term I just made up. It’s something like a call for papers, except that I’m instead looking for random external kicks in the form of suggestions, life advice of any level of quality and thought-out-ness, clarifying questions, whatever. Anything that helps me frame the problem differently and get out of the rather stale old loop of thoughts that I’m currently stuck in. I guess the only constraint is that I’d prefer positive ‘have you considered X?’ to negative ‘I think that Y is a bad idea’.
I have some writing stuff I want to finish as well. I’ve been converting my newsletter posts on The Roots of Romanticism into a more polished blog post and should finish that soon. I’ve also been reading Derrida’s Speech and Phenomena and it’s been going weirdly well, I actually understand a surprising amount of it and haven’t got too frustrated with his style. So I might attempt to write up some of what I learned.
Anyway feel free to email me, or comment, or whatever, if you have a response for my call for perturbations. Some more context in the old linked post - I think most of it still applies.



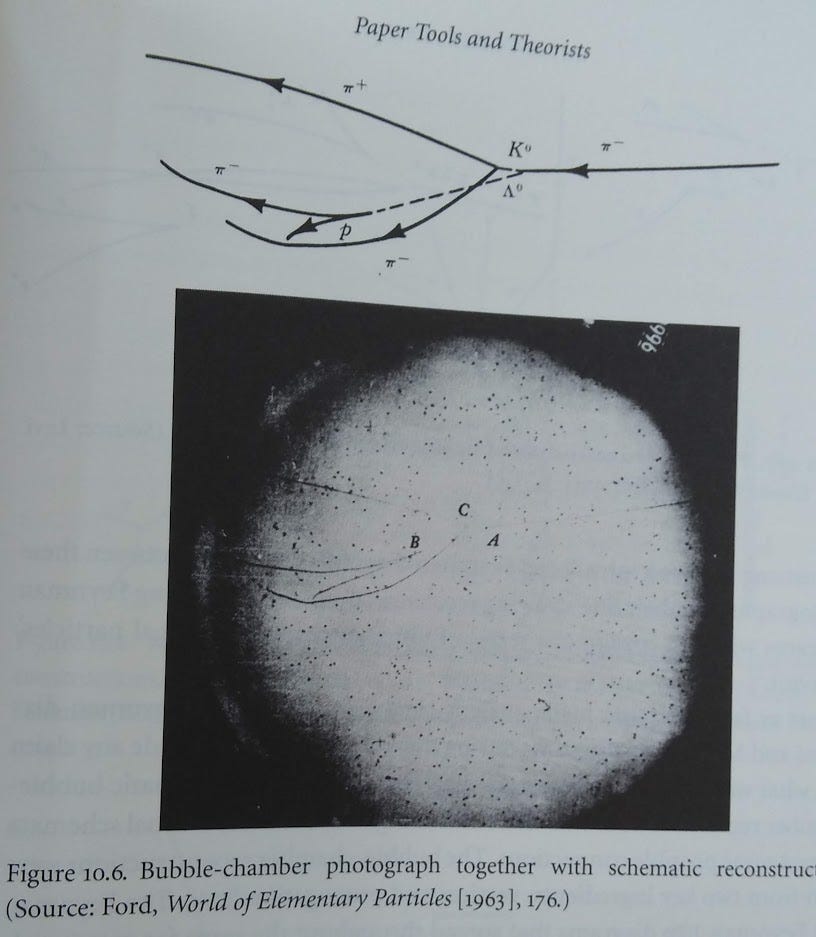
This made me realize that I had always implicitly and vaguely assumed that Feynman diagrams are stylized versions of the bubble chamber tracks. They aren't? (I know basically zip about the diagrams except that they condense boilerplate perturbation hair in some a convenient way. I guess on reflection that doesn't seem to have much to do with the tracks? Sorry to be stupid, I don't know any physics almost.)
Oh, this is really weird, I totally didn't get your punning on "perturbation." I have a cheddar and spinach casserole for brains.