January 2024: relativity cooked three ways
Unusual reframings of special relativity
Hi again. In the last few months I’ve been reading various bits and pieces to do with special relativity, and I’m going to try and patch them into a semi-coherent newsletter post.
I find the literature on special relativity interesting. The formal structure of special relativity is very elegant and self-contained. It’s not really an area of research specialisation, exactly, more like background machinery that’s used in other areas of physics, and so you aren’t likely to see new research papers that are just about special relativity. But people are still thinking about how to explain special relativity. Partly because there are always new physics students who need to learn the background machinery to do other things, and partly because it’s just a cool subject with weird results that isn’t too mathematically intense, so it’s a great topic for a “physics can be interesting actually” sort of course. This pressure to find clear, straightforward ways of teaching the subject has led to some nice reframings.
In this newsletter I’m going to talk about three unusual approaches to introducing special relativity. Actually explaining these in any depth would make for a very long newsletter, and I have in no way left myself time for that, so what I’m going to do instead is give a very rough description of what they are and link out to sources. Mainly I’m trying to convey “look there’s something cool here” rather than “here’s exactly how it works”.
I’m also going to assume you know something about special relativity, basically the idea of time dilation and length contraction and the fact that velocities add together weirdly. For the last of the three approaches I’ll also talk a bit about Minkowski space.
(If you don’t know anything about special relativity, and you want to, and you’re happy with maths at the level of doing Pythagoras and rearranging equations with squared terms in them, then maybe you can learn the necessary background pretty quickly? For example, you could follow the derivation of time dilation on this Wikipedia page section, or if you want more words you could try this, I’ve only skimmed it but John Norton is normally very good at explaining things. For Minkowski space, I’m not sure what the best intro is but again John Norton has written something that looks good.)
Anyway here are the three approaches, in order of increasing weirdness.
Bondi: Relativity and Common Sense
This is a 1964 popular book by the relativist Hermann Bondi that I read recently. It’s very clearly written and emphasises the continuity between relativity and classical physics, rather than trying to make everything sound as weird and new as possible. So he starts with a lot of discussion of classical-physics stuff like Galilean relativity and the Doppler effect.
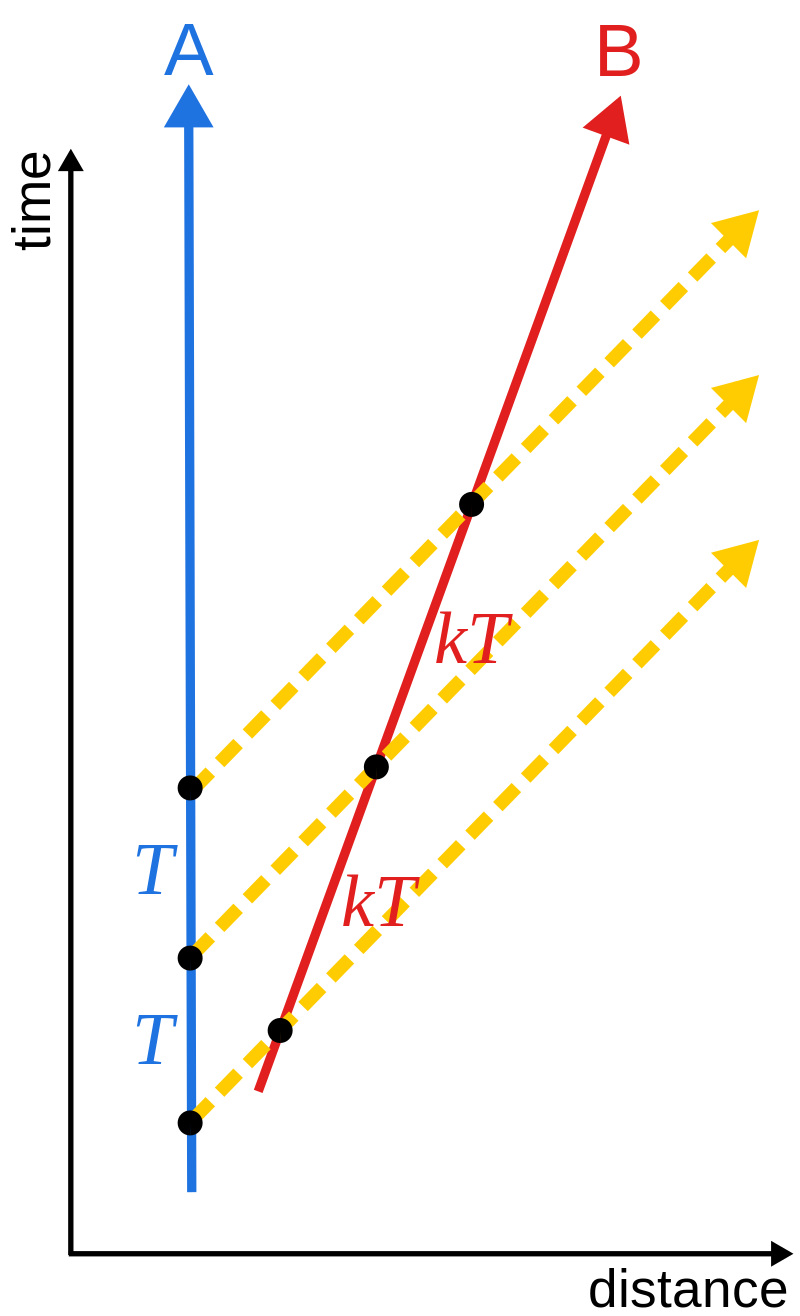
The main unusual feature of this book is his route to deriving the results of special relativity, which has become known as the Bondi k-calculus. It centres round this quantity k which is probably best understood by seeing a diagram (source):
You have some guy A with a torch sending out constant flashes T seconds apart, and some other guy B moving away at constant velocity who receives them kT seconds apart.1 Bondi then uses more complicated setups with multiple observers to build up the usual results of special relativity in terms of this k quantity.
There’s something about the concreteness of this approach that I appreciate. It’s helped me think more clearly about how coordinates in special relativity relate to what we actually measure.
Mermin and Sen on relativity without light
Relativity is normally derived from two postulates, the principle of relativity (physics looks the same in all inertial frames) and the constancy of the speed of light. These always felt very different in my head: the first makes a lot of sense, whereas the second one is intuitively surprising.
It turns out you can do without the second one! You do have to make some other assumptions instead, to do with homogeneity of spacetime and isotropy of space, but these are less surprising feeling.
The best known paper on this is probably Mermin’s Relativity without light, which is another of the collected papers in the Boojums book I wrote about last time. He wasn’t the first person to notice (looks like it was Ignatowsky back in 1910, five years after special relativity was invented!), but I still recommend his paper for the introduction and context, and the distinctive Mermin writing style. His derivation is more complicated than some others, though. My favourite version of the derivation is Achin Sen’s How Galileo could have derived the special theory of relativity, which is particularly simple. And if I remember correctly (it’s been a while since I read these, Lévy-Leblond’s One more derivation of the Lorentz transformation makes the assumptions particularly clear.
As I remember it the papers all derive the velocity addition law first, by starting with a general law
and then adding on symmetry requirements to constrain it to look like this:
The K < 0 case is kind of interesting and turns out to map to rotations of space and time, so you can end up pointing in the opposite direction of time to where you started. So that gets ruled out for causality reasons, leaving K = 0 and K > 0.
The K > 0 case matches special relativity, with K = 1/c^2. For K = 0 you get the good old classical law, w = u + v. So I guess you do still have to distinguish between those with actual measurements, but you’ve constrained the form pretty closely.
Epstein: Relativity Visualized
Lewis Carroll Epstein is I think best known for his book Thinking Physics, which teaches classical physics in a conceptual, problem-based way. (I have not got a copy yet, though I keep meaning to. Some of the Less Wrong people seem to rate it highly.) His approach to explaining special relativity in his book Relativity Visualized is the biggest departure from the “standard” approach of the three, by some way. It’s also the one I’ve thought about least, and I’m still wrapping my head around it, so this section is particularly undigested.
Maybe the quickest way to introduce it starting from the standard approach is to take the Minkowski metric that gives proper time in terms of coordinate time and space,
and then rearrange it to get
Now we’ve got a normal Euclidean metric in proper time and coordinate space, and can just calculate distances in the standard way. Simple!
It’s probably occurred to you at this point that physicists generally know basic school algebra, and that if it was a straightforwardly good idea to move a term to the other side, they’d have done it by now. So, no, it’s not a straightforwardly good idea and there’s actually considerable weirdness here. The proper time tau is not a path-independent coordinate like t and x; instead, it’s an arc length along a particular path and so it’s path-dependent. Each observer measures a different proper time. You can make diagrams anyway if you’re happy to draw them from the perspective of a single observer, with tau as the distance along their worldline, and it looks like that’s what Epstein does. For more details on the coordinate thing and a longer review of Epstein’s book, I recommend this blog post by Michael Weiss.
Epstein’s own approach to explaining this idea is more colourful:
To understand the Special Theory of Relativity at the gut level, a good myth must be invented, and here it is…
Why can’t you travel faster than the speed of light? THE REASON YOU CAN’T GO FASTER THAN THE SPEED OF LIGHT IS THAT YOU CAN’T GO SLOWER. THERE IS ONLY ONE SPEED. EVERYTHING, INCLUDING YOU, IS ALWAYS MOVING AT THE SPEED OF LIGHT.
Given that I’m only quoting this one thing from the book, I should maybe point out that the rest of it is not shouting in all caps about something slightly insane sounding. It’s eccentric and distinctive but not unhinged crankery. In context I think the point of this “myth” framing and the yelling is to clearly signal “I’m not being too serious here”, to stop people getting too hung up immediately on whether this reframing is really truly true and just get them thinking through the implications for a bit.
Maybe this diagram from the Michael Weiss blog post makes the point of the myth a bit clearer. It also links us back to the stuff about metrics and proper time. That diagram is a space-proper-time diagram of a single “observer” (a rock, in this case), and as we saw above it’s a Euclidean space. The idea is that the rock, the rocket and the photon all “travel at the same speed”, according to Epstein’s weird definition of speed, over a period of the rock’s proper time (let’s say one day) and end up the same distance from the origin of the graph. The rock is doing all that travelling in proper time and ages by a day. The photon is travelling purely through space and doesn’t age at all. And the rocket is doing something in between and ages less than the rock. So this is where time dilation comes in. See the diagrams in another blog post by Andrew Macdonald for more explanation.
As I said at the start, I’m still reading the book and digesting this idea. It looks like Epstein takes the approach pretty far, getting to gravity and black holes in later chapters. But so far I haven’t internalised it to the point that I feel like I “get it”.
Other things this month
I didn’t make notes on what I read or did this month, so I’ve mostly forgotten and this section is going to be short:
The biggest new thing for me was going to an Alexander Technique workshop in London run by Peter Nobes. His approach to the Alexander Technique has been popularised by Michael Ashcroft online and is supposed to go well with the style of opening awareness meditation I’m practising, so I’ve been intrigued for a while now. There’s definitely something interesting there and I’m planning to do more of it.
The Inner Game of Tennis came up in the workshop so I’m reading that.
While researching the Epstein part of this post I found a weird self-published book, Epstein explains Einstein. Mainly notable because the author is called Eckstein and the translator is called Edelstein. Wtf?
Next month
I’m thinking of reviving the notebook and getting out at least a couple of short posts there. Also probably more Alexander Technique stuff and more reading the Epstein book.
I might also make the newsletter worse? According to my description this is supposed to be a “workbook for half-baked ideas”, but something about the Substack format makes me end up baking them more. Maybe this is better for the reader, I don’t know, but it takes more time and makes me default to explaining things I at least half understand already. I’d rather be learning what I think by writing, rather than saying stuff I already know.
In the book they’re called Alfred and Brian. The 1964 version of Alice and Bob.


This website provides a unique understanding of physics and relativity.
http://www.artandphysics.com